APL is one of the most curious programming languages you’ll ever run across. For example, take a random problem out of Rosetta Code: “Numbers divisible by their individual digits, but not by the product of their digits.”. Here’s a typical implementation in C:

#include <stdio.h>

int divisible(int n) {
    int p = 1;
    int c, d;

    for (c=n; c; c /= 10) {
        d = c % 10;
        if (!d || n % d) return 0;
        p *= d;
    }

    return n % p;
}

int main() {
    int n, c=0;

    for (n=1; n<1000; n++) {
        if (divisible(n)) {
            printf("%5d", n);
            if (!(++c % 10)) printf("\n");
        }
    }
    printf("\n");

    return 0;
}

I wrote some PowerShell to take a look at the lengths of the solution in different languages, and as you would expect - there is quite a difference in verbosity.

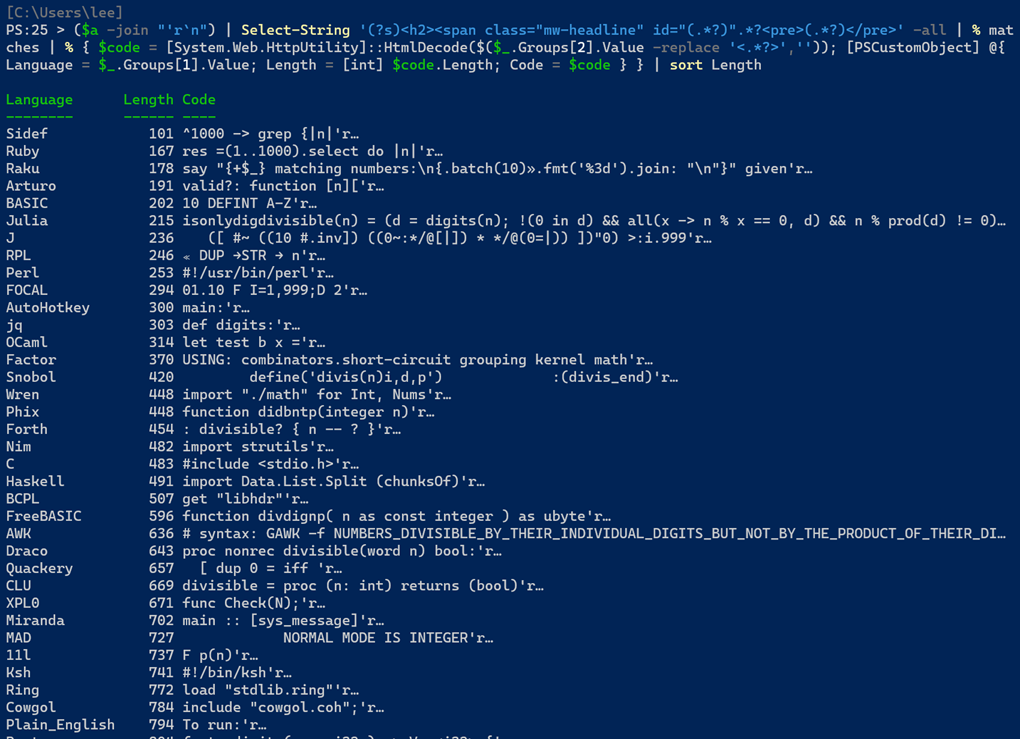
But I left one out. APL.

(⊢(/⍨)((⍎¨∘⍕)((∧/0=|)∧0≠(×/⊣)|⊢)⊢)¨)⍳999

Madness! 43 characters. Almost none of which you see or use in any other programming language. But the symbols are really just short function names for things you are probably already familiar with in other languages, such as ⍳ (Iota), which means “generate a list of numbers”, and ¨ (Diaeresis) which means “foreach”. You read APL mostly right-to-left, so the start of the little snippet above means “Generate a list of numbers from 1 to 999. For each of those, do what follows.”

Additionally, APL programs flow very much like pipelines that you probably have experience with in PowerShell or Bash. The output of one stage usually becomes the input for the next.

If you’re interested in checking out APL, here are three great resources:

• Text-based tutorial: Learning APL

• Online APL playground: TryAPL

• Dyalog APL download: Dyalog APL

Conway’s Game of Life

Code_Report on YouTube has a bunch of great videos explaining the thought process for a bunch of APL programs, and one absolute masterclass is his explanation of the implementation of Conway’s Game of Life.

⍝ Conway's Game of Life

⎕IO←0

lifeInit ← {?2⍴⍨1 2×⍵}
lifeIter ← {⊃1 ⍵∨.∧3 4=+/+⌿1 0 ¯1∘.⊖1 0 ¯1⌽¨⊂⍵}
life     ← '.⌽'[t←lifeInit 10]
{} {life∘←'.⌽'[⍵] ⋄ _←⎕DL÷8 ⋄ lifeIter ⍵}⍣≡t

Which generates this magic:

After seeing that, I knew it was time for APL to get a demoscene. Namely, the famous fire effect.

Here’s a deep series on implementing this in PowerShell: Burn-Console.

Demoscene Fire Effect in APL

Without further ado, here’s a Fire Effect in APL in all of its glory:

⎕IO  ← 0
iter ←{⍉(≢⍉⍵)↑⍉(≢⍵)↑1⊖1⌽1⊖⊃9.05÷⍨+/+⌿1 0 ¯1∘.⊖1 0 ¯1⌽¨⊂¯1⊖¯1⌽(
   (≢⍵)+2)↑⍉((≢⍉⍵)+2)↑⍉⍵⍪28+228×?2⍴⍨≢⍵}
{}{canvas∘←170↓'   +=*░#▒▓'[(⌊(⍵÷10))⌊9]⋄_←⎕DL÷32⋄iter ⍵}⍣≡0⍴⍨1 1×250

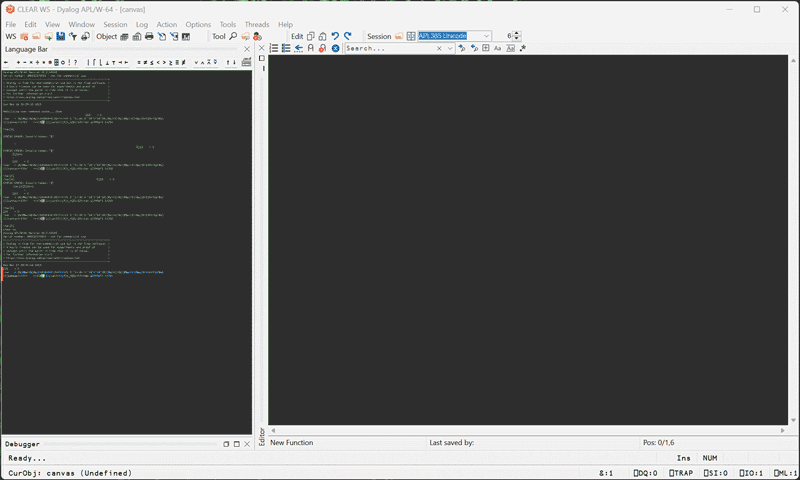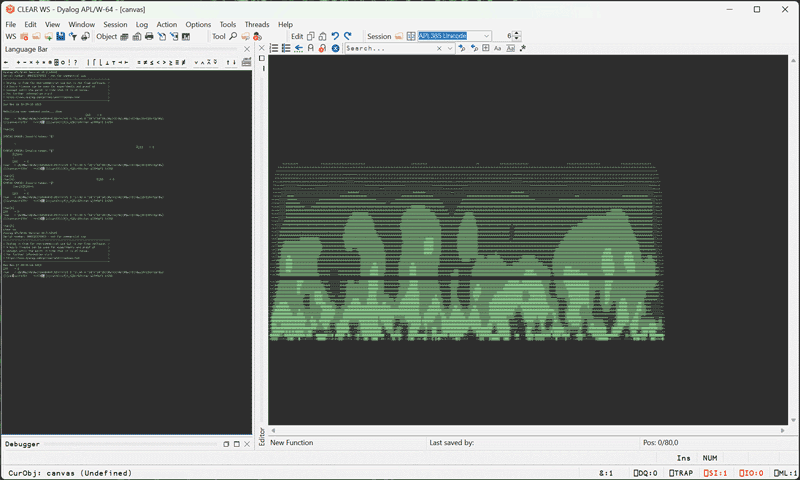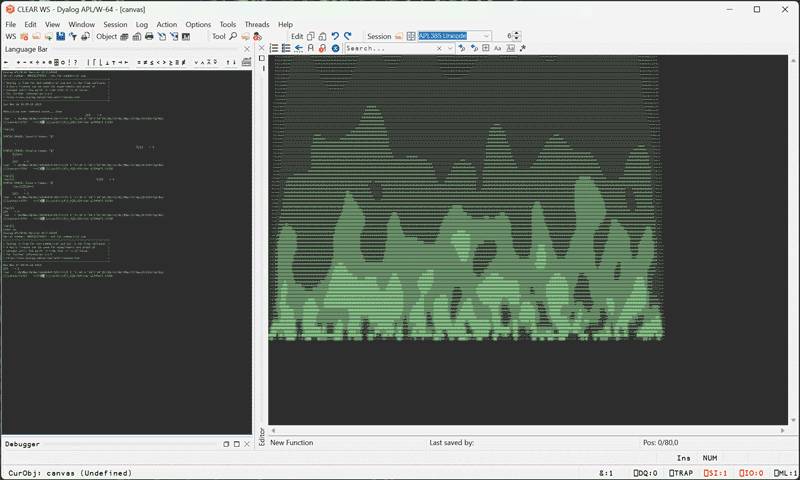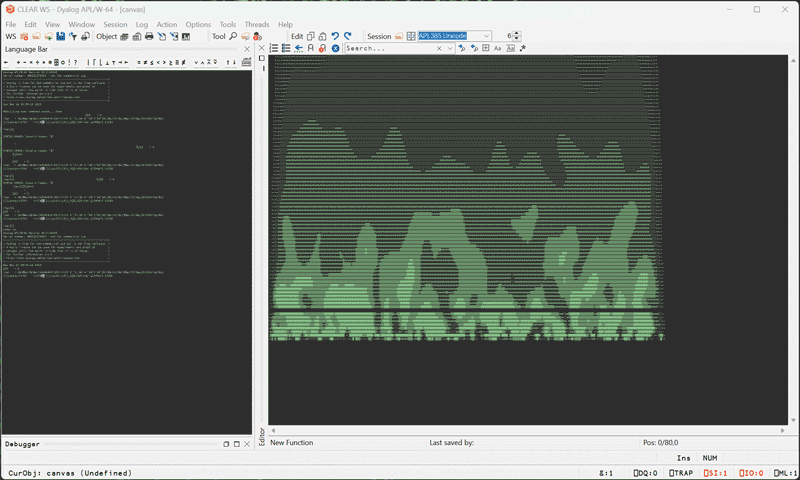
APL is absolutely incredible.

Understanding the Code

Here’s a rough outline of what the code is doing.

⎕IO  ← 0

Sets APL to use 0 as its array indexing basis, rather than the default of 1.

iter ←{⍉(≢⍉⍵)↑⍉(≢⍵)↑1⊖1⌽1⊖⊃9.05÷⍨+/+⌿1 0 ¯1∘.⊖1 0 ¯1⌽¨⊂¯1⊖¯1⌽(

    (≢⍵)+2)↑⍉((≢⍉⍵)+2)↑⍉⍵⍪28+228×?2⍴⍨≢⍵}

Defines a function that the next line will use. We’ll talk about that in a second.

{}{canvas∘←170↓'   +=*░#▒▓'[(⌊(⍵÷10))⌊9]⋄_←⎕DL÷32⋄iter ⍵}⍣≡0⍴⍨1 1×250

Creates and manages the canvas, as well as the loop that updates it. Here is that code broken out with a bit more detail - remember, you read right-to-left:

Now, here’s what that iter function does:

There are a few optimizations you could make if you were really trying to code golf this solution at the cost of making the solution less generic. But at 167 characters, it’s tight enough for my taste :)